The Farey framework for SL2-tilings
This website is devoted to the project on using a combinatorial approach to explore the connections between number theory and geometry that arise around Conway–Coxeter friezes and SL2-tilings over integer numbers and other rings, carried out at the Open University, UK.
August 2025 highlights
- New short note preprint: Wildest SL2-tilings.
- Save the dates: Farey’s legacy in frieze patterns and discrete geometry workshop, ICMS, Edinburgh, 20–24 April 2026.
- Triangulations and friezes, an interactive demonstration of the connections between triangulated polygons, paths in the Farey graph, friezes, and cluster variables in the cluster algebra of type An, now can also be found at the Visual Cluster Algebras portal, together with other CA-related apps (although the updates appear here first, for now).
Gallery
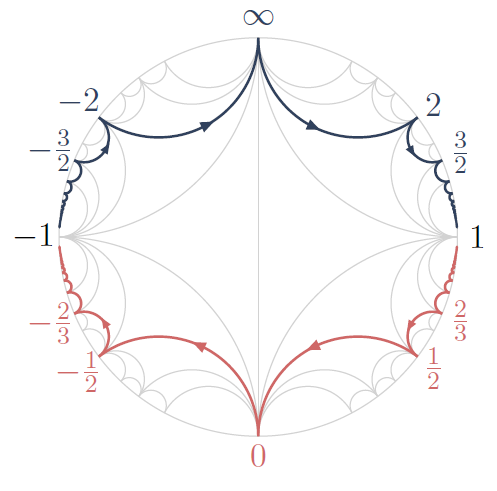
Two paths in the Farey graph in the Poincaré disk, corresponding to a certain SL
2-tiling
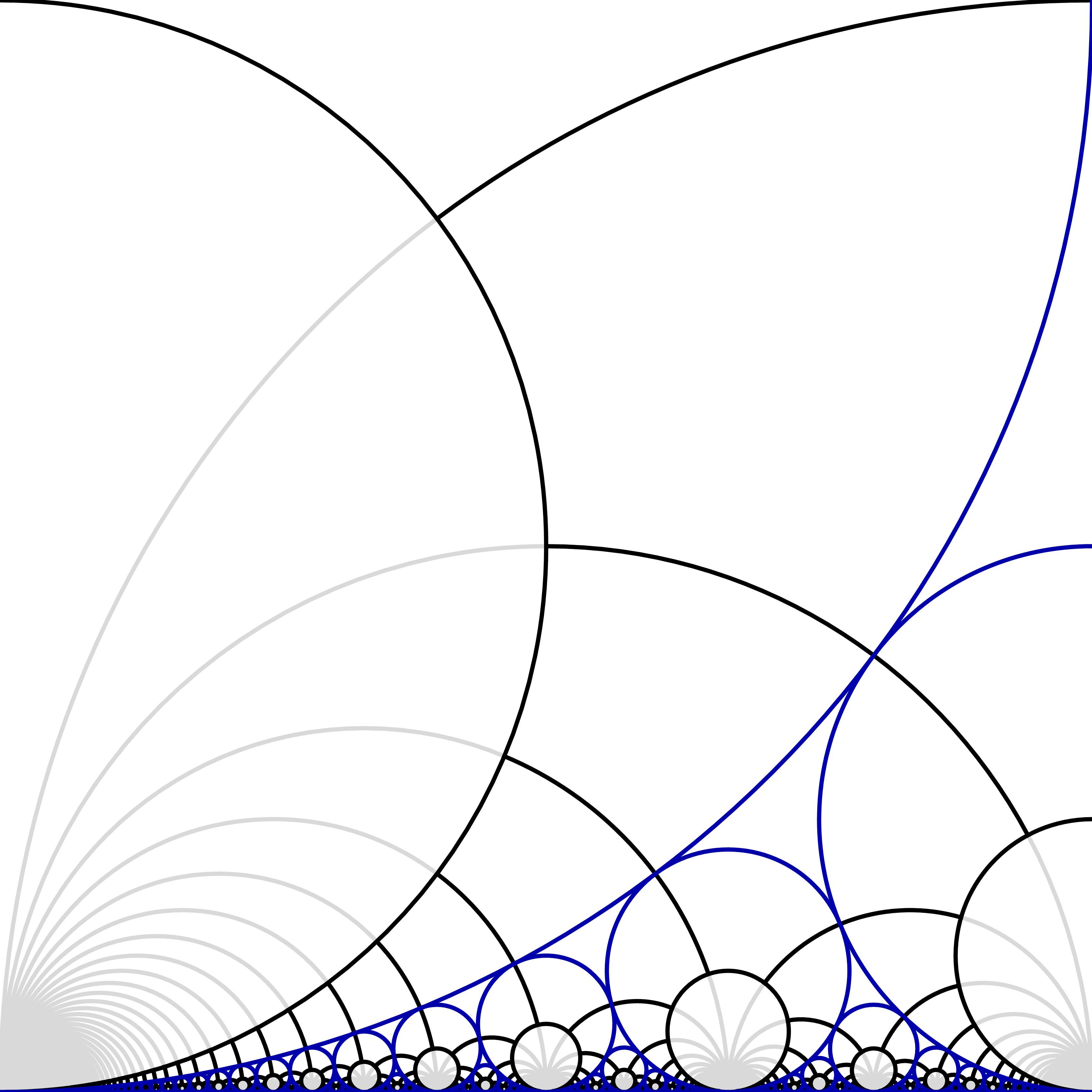
Portions of the Farey graph (grey), Ford circles (blue), and the truncated Farey graph (black) in the upper half-plane
An SL
2-tiling with the greatest possible wild density and unbounded rank
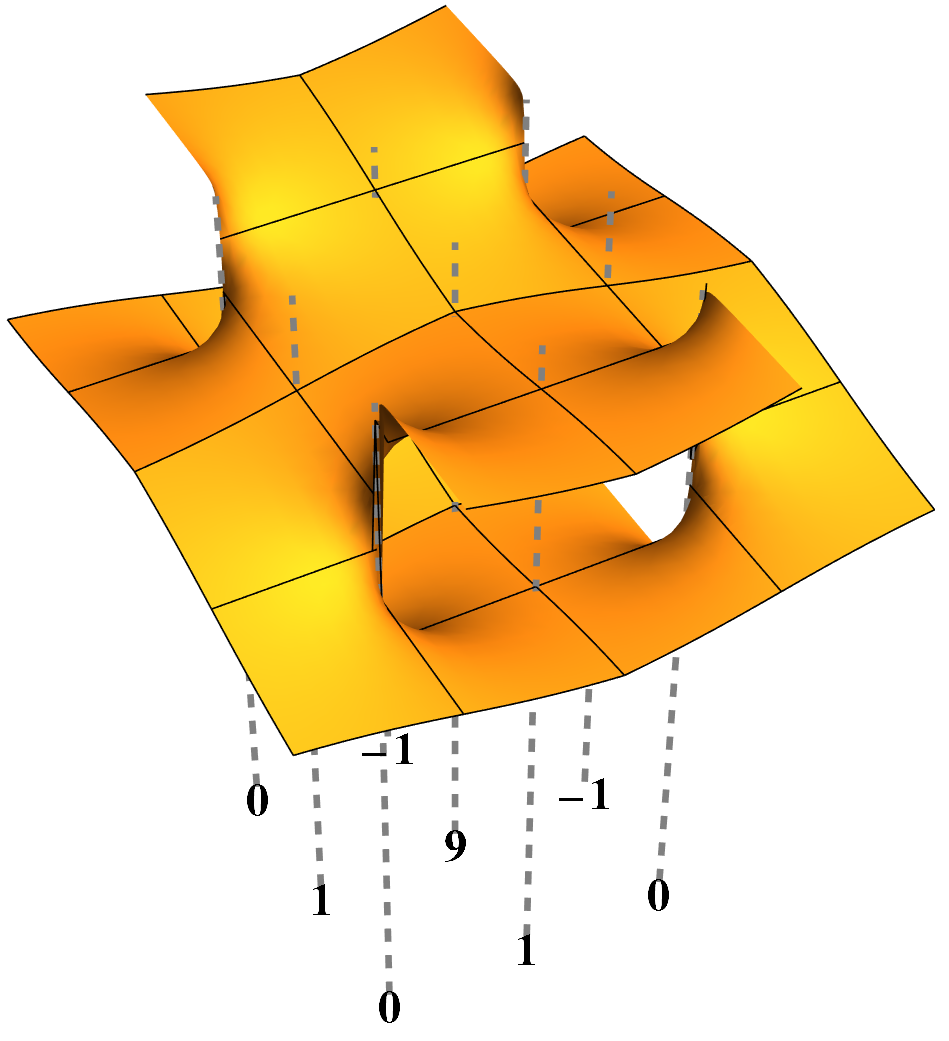
Farey surface of a certain wild SL
2-tiling
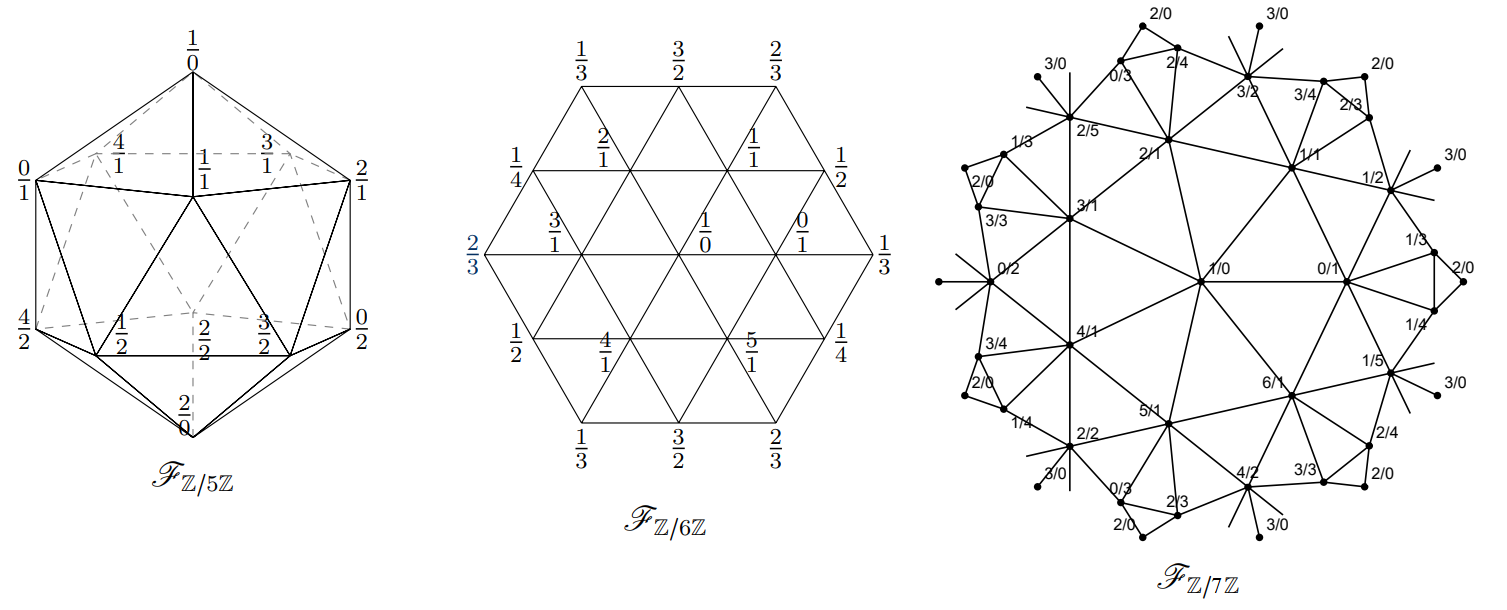
The Farey complexes over integers modulo 5, 6, 7: icosahedron, hexagonal torus, Klein quartic
The project is funded by EPSRC grants EP/W002817/1, EP/W524098/1, and EP/T518165/1 (S.B.'s internship).
SL2-tilings